Integer Overflows and Underflows
Contents
Description
- Integer overflows and underflows are made possible by the way numbers are handled in computer memory.
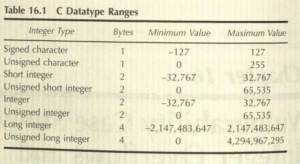
- Each hit in computer memory has only possible values, 1 or 0, and different numbers of bytes (units of 8 bits) are used to store integers based on the size of the number to be stored.
- If no negative numbers are needed, a signed datatype will often be used. In a signed datatype, the value is always positive, and a larger positive number can be stored in the same number of bytes than can be stored using an unsigned datatype because the first bit is not reserved to Indicate whether the integer is positive or negative.
- The ranges of some common C datatypes are shown in the table.
- Integer math is handled with a method called twos complement arithmetic. This, along with fact that computers are very literal, can cause a security vulnerability. When told to add or subtract, they do so based on this specialized type of arithmetic with no regard to whether the results make logical sense.
- This method of doing arithmetic is used on almost all systems because the overhead of doing floating point math is so high.
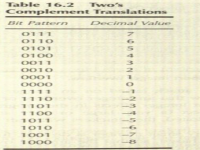
- In two's complement, if you are dealing with a signed integer datatype: the binary value can be translated directly to decimal, and nothing special needs to be done. If you are using an unsigned datatype, and the leftmost bit (the one that indicates the sign of the number) is a 0, then your number is positive and can be translated directly to decimal.
- If, however, it is a negative number, then the following must be done to obtain an accurate decimal translation.
- First the two's complement needs to be translated back to normal binary. Starting with the rightmost (least significant) bit, copy the bit pattern of the two’s complement number until you copy the first bit that is one.
- Then, write down the complements of the remaining digits.
- If the original bit was a one, write down zero and vice versa.
- Once two’s complement has been translated back to a standard binary number. you can translate it to decimal using normal rules and then add a negative sign.
- When integer math is performed, the appropriate bits are flipped , but the result incrementing a large positive number can be a large negative number or zero.
- The result of decrementing a large negative number can be a large positive number.
- If the results require that another bit than is available in the datatype be allocated, the leftmost digit is simply truncated.
- Two samples of incrementing and decrementing are shown in the following two figures, respectively.
Anatomy of an Exploit
- Integer overflows are most useful as a way to set up for stack overflow if the attacker is able to create an integer overflow in a variable that is latter used in the dynamic allocation of memory.
- Because no widespread exploits are in the wild, an attack is pretty much based on logic and conjecture.
- To carry out an attack based on an integer overflow, the attackers would need to know that an integer overflow or underflow vulnerability exists and what that integer affects in the program under attack.
- Based on the desired effect (a very large or very small number) after the vulnerability is exploited, the attackers will craft their exploit to achieve that end.
- Sometimes, a very small number is desired, for example, the quantity of items being purchased. so that the amount owed is very small, zero or even negative (which would result in a credit to the buyer).
- A number can also be desired if that number is used to determine how large a buffer to allocate. and later a large number is stored in that undersized buffer.
- Sometimes, a very large number is desired to create buffer overrun or similar situation in which the number is the length of something being transmitted or stored and will result in overrun when it is later stored in a buffer that was expected to hold something smaller.
- The attacker can also attempt to force the integer to contain a zero by either integer underflow or overflow so as to cause a division by zero or some other error when a code that doesn't expect a zero attempt to process one.
Real-World Examples
- No widespread exploits have been reported as being based on an integer overflow, but quite a few vulnerabilities have been reported and Patched especially in the last few years. This is only smart because there will certainly be attention paid to how to successfully exploit the known vulnerability.
Test Techniques
Black Box
- Black-box testing of integer overflows and underflows is very difficult. All variables still need to be examined, and the tester should know or discover what calculations are carried out with those variables and then attempt to influence those results.
- Sometimes you will seemingly get no response; sometimes you will get an error message that gives more clues to the actual datatype being used. The ranges typically returned in some of these error messages can often be translated directly into datatype range Values, thus revealing a potentially useful bit of data to the attackers but also to the tester.
- Try to set the variable to a maximum or minimum value and then try to increment the maximum or decrement the minimum.
- Always try long strings in input fields and remember that “long' tends to be a rather fluid description.
- Always try the largest and smallest allowable values in numeric fields to see if there is a case in which the individual integers are correctly checked but perhaps operations performed with them are not.
- Always verify the data coming from other sources for the same flaws as data being input directly into the program itself. All trust is misplaced.
- Don’t forget applications programming interface (API) calls and methods of passing data other than the user interface (UI).
- Never trust what calling your functionality to do so correctly and with the correct data. trust is misplaced.
- Your program needs to be able to protect itself.
White Box
- There are several places in a code where an integer underflow or overflow can occur. These include:
- Arithmetic operations
- Conversions and casts
- Copying and reading
- If the expected value of a variable is easily defined, the variable should he checked for that value or range/size before it is used or stored. This allows the system to protect itself, at least in part.
- All integer values need to be followed through the system to examine the bounds of each variable and then the bounds possible (not just expected) when an arithmetic operation or cast is carried out.
- Then, take combinations of the maximum values of each variable and carry out the operation to determine if the resulting value is larger or smaller than the resulting integer type.
- Next, carry out the same process using combination of the smallest possible values and check the result of that against the resulting integer type as well.
External Links
Panel title
Percipit Mnesarchum
Molestie Phaedrum Luptatum
constituam Habeo adipisci Inani
zril Forensibus sea Habeo
adipisci Minimum corrumpit Regione
suscipit Has et partem Percipit
Mnesarchum Molestie Phaedrum
Luptatum constituam Habeo
adipisci Inani zril Vel
nisl albucius Habeo adipisci Minimum
corrumpit Regione suscipit Percipit
maiestatis Regione suscipit Percipit
maiestatis
Subtitle